Общее уравнение плоскости имеет вид. Различные виды уравнения плоскости

12.1. Основные понятия

Поверхность и ее уравнение

Поверхность в пространстве можно рассматривать как геометрическое место точек, удовлетворяющих какому-либо условию. Например, сфера радиуса R с центром в точке О 1 есть геометрическое место всех точек пространства, находящихся от точки O 1 на расстоянии R.

Прямоугольная система координат Oxyz в пространстве позволяет установить взаимно однозначное соответствие между точками пространства и тройками чисел х, у и z - их координатами. Свойство, общее всем точкам поверхности, можно записать в виде уравнения, связывающего координаты всех точек поверхности.

Уравнением данной поверхности в прямоугольной системе координат Oxyz называется такое уравнение F(x, у, z) = 0 с тремя переменными х, у и z, которому удовлетворяют координаты каждой точки, лежащей на поверхности, и не удовлетворяют координаты точек, не лежащих на этой поверхности. Переменные х, у и z в уравнении поверхности называются текущими координатами точек поверхности.

Уравнение поверхности позволяет изучение геометрических свойств поверхности заменить исследованием его уравнения. Так, для того, чтобы узнать, лежит ли точка M 1 (x 1 ;y 1 ;z 1) на данной поверхности, достаточно подстави ть координаты точки M 1 в уравнение поверхности вместо переменных: если эти координаты удовлетворяют уравнению, то точка лежит на поверхности, если не удовлетворяют - не лежит.

Уравнение сферы

Найдем уравнение сферы радиуса R с центром в точке O 1 (x 0 ;y 0 ;z 0). Согласно определению сферы расстояние любой ее точки М(х; у; z) от центра O 1 (x 0 ;y 0 ;z 0) равно радиусу R, т. е. O 1 M= R. Но , где . Следовательно,

Это и есть искомое уравнение сферы. Ему удовлетворяют координаты любой ее точки и не удовлетворяют координаты точек, не лежащих на данной сфере.

Если центр сферы Ο 1 совпадает с началом координат, то уравнение сферы принимает вид .

Если же дано уравнение вида F(x;y;z) = 0 , то оно, вообще говоря, определяет в пространстве некоторую поверхность.

Выражение «вообще говоря» означает, что в отдельных случаях уравнение F(x; y; z)=0 может определять не поверхность, а точку, линию или вовсе не определять никакой геометрический образ. Говорят, «поверхность вырождается».

Так, уравнению не удовлетворяют никакие действительные значения х, у, z. Уравнению удовлетворяют лишь координаты точек, лежащих на оси Ох (из уравнения следует: у = 0, z = 0, а х - любое число).

Итак, поверхность в пространстве можно задать геометрически и аналитически. Отсюда вытекает постановка двух основных задач:

1. Дана поверхность как геометрическое место точек. Найти уравнение этой поверхности.

2. Дано уравнение F(x;y;z) = 0. Исследовать форму поверхности, определяемой этим уравнением.

Уравнения линии в пространстве

Линию в пространстве можно рассматривать как линию пересечения двух поверхностей (см. рис. 66) или как геометрическое место точек, общих двум поверхностям.

Если и - уравнения двух поверхностей, определяющих линию L, то координаты точек этой линии удовлетворяют системе двух уравнений с тремя неизвестными:

(12.1)

Сравнения системы (12.1) называются уравнениями линии в пространстве. Например, есть уравнения оси Ох.

Линию в пространстве можно рассматривать как траекторию движения точки (см. рис. 67). В этом случае ее задают векторным уравнением

или параметрическими уравнениями

проекций вектора (12.2) на оси координат.

Например, параметрические уравнения винтовой линии имеют вид

Если точка Μ равномерно движется по образующей кругового цилиндра, а сам цилиндр равномерно вращается вокруг оси, то точка Μ описывает винтовую линию (см. рис. 68).

12.2. Уравнения плоскости в пространстве

Простейшей поверхностью является плоскость. Плоскость в пространстве Oxyz можно задать разными способами. Каждому из них соответствует определенный вид ее уравнения.

Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

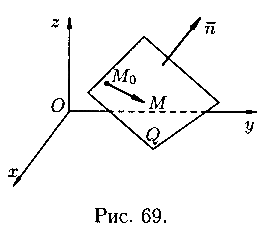
Пусть в пространстве Oxyz плоскость Q задана точкой и вектором , перпендикулярным этой плоскости (см. рис. 69). Выведем уравнение плоскости Q. Возьмем на ней произвольную точку и составим вектор . При любом расположении точки Μ на плоскости Q векторы и взаимно перпендикулярны, поэтому их скалярное произведение равно нулю: , т. е.

(12.3)

Координаты любой точки плоскости Q удовлетворяют уравнению (12.3), координаты точек, не лежащих на плоскости Q, этому уравнению не удовлетворяют (для них ).

Уравнение (12.3) называется уравнением плоскости, проходящей через данную точку перпендикулярно вектору . Оно первой степени относительно текущих координат x, y, z. Вектор называется нормальным вектором плоскости.

Придавая коэффициентам А, В и С уравнения (12.3) различные значения, можно получить уравнение любой плоскости, проходящей череp точку . Совокупность плоскостей, проходящих через данную точку, называется связкой плоскостей, а уравнение (12.3) - уравнением связки плоскостей.

Общее уравнение плоскости

Рассмотрим общее уравнение первой степени с тремя переменными х, у и z:

Полагая, что по крайней мере один из коэффициентов А, В или С не равен нулю, например , перепишем уравнение (12.4) в виде

Сравнивая уравнение (12.5) с уравнением (12.3), видим, что уравнения (12.4) и (12.5) являются уравнением плоскости с нормальным вектором , проходящей через точку .

Итак, уравнение (12.4) определяет в системе координат Oxyz некоторую плоскость. Уравнение (12.4) называется общим уравнением плоскости.

Частные случаи общего уравнения плоскости:

1. Если D = 0, то оно принимает вид . Этому уравнению удовлетворяет точка . Следовательно, в этом случае плоскость проходит через начало координат.

2. Если С = 0, то имеем уравнение . Нормальный вектор перпендикулярен оси Οz. Следовательно, плоскость параллельна оси Οz; если B = 0 - параллельна оси Оу, А = 0 - параллельна оси Ох.

3. Если С = D = 0, то плоскость проходит через параллельно оси Οz, т. е. плоскость проходит через ось Οz. Аналогично, уравнениям и отвечают плоскости, проходящие соответственно через оси Ох и Оу.

4. Если А = В = 0, то уравнение (12.4) принимает вид , т. е. Плоскость параллельна плоскости Оху. Аналогично, уравнениям и отвечают плоскости, соответственно параллельные плоскостям Oyz и Οxz.

5. Если A = B = D = 0, то уравнение (12.4) примет вид , т. е. z = 0. Это уравнение плоскости Оху. Аналогично: у = 0 - уравнение плоскости Οxz; x = О - уравнение плоскости Oyz.

Уравнение плоскости, проходящей через три данные точки

Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M 1 (x 1 ;y 1 ;z 1), М 2 (x 2 ;y 2 ;z 2) и М 3 (х 3 ,y 3 ,z 3), не лежащие на одной прямой.

Возьмем на плоскости произвольную точку M(x;y;z) и составим векторы , , . Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем , т. е.

(12.6)

Уравнение (12.6) есть уравнение плоскости, проходящей через три данные точки.

Уравнение плоскости в отрезках

Пусть плоскость отсекает на осях Ох, Оу и Оz соответственно отрезки a , b и c , т. е. проходит через три точки A(a;0;0) , B(0;b;0) и C(0;0;c) (см.рис. 70). Подставляя координаты этих точек в уравнение (12.6), получаем

Раскрыв определитель, имеем , т. е. или

(12.7)

Уравнение (12.7) называется уравнением плоскости в отрезках на осях. Им удобно пользоваться при построении плоскости.

Нормальное уравнение плоскости

Положение плоскости Q вполне определяется заданием единичного вектора , имеющего направление перпендикуляра ОК, опущенного на

плоскость из начала координат, и длиной p этого перпендикуляра (см. рис. 71).

Пусть ОК = p , а α, β, g - углы, образованные единичным вектором ё с осями Ох, Оу и Οz. Тогда . Возьмем на плоскости произвольную точку М(х; у; z) и соединим ее с началом координат. Образуем вектор . При любом положении точки Μ на плоскости Q проекция радиус-вектора на направление вектора всегда равно р: , т. е. или

(12.8)

Уравнение (12.8) называется нормальным уравнением плоскости в векторной форме. Зная координаты векторов f и e , уравнение (12.8) перепишем в виде

Уравнение (12.9) называется нормальным уравнением плоскости в координатной форме.

Отметим, что общее уравнение плоскости (12.4) можно привести к нормальному уравнению (12.9) так, как это делалось для уравнения прямой на плоскости. А именно: умножить обе части уравнения (12.4) на нормирующий множитель , где знак берется противоположным знаку свободного члена D общего уравнения плоскости.

Все уравнения плоскости, которые разобраны в следующих пунктах могут быть получены из общего уравнения плоскости, а также приведены к общему уравнению плоскости. Таким образом, когда говорят об уравнении плоскости, то имеют в виду общее уравнение плоскости, если не оговорено иное.

Уравнение плоскости в отрезках.

Уравнение плоскости вида , где a , b и c – отличные от нуля действительные числа, называется уравнением плоскости в отрезках .

Такое название не случайно. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекает плоскость на координатных осях Ox , Oy и Oz соответственно, считая от начала координат. Знак чисел a , b и c показывает, в каком направлении (положительном или отрицательном) следует откладывать отрезки на координатных осях.

Для примера построим в прямоугольной системе координат Oxyz плоскость, определенную уравнением плоскости в отрезках . Для этого отмечаем точку, удаленную на 5 единиц от начала координат в отрицательном направлении оси абсцисс, на 4 единицы в отрицательном направлении оси ординат и на 4 единицы в положительном направлении оси аппликат. Осталось соединить эти точки прямыми линиями. Плоскость полученного треугольника и есть плоскость, соответствующая уравнению плоскости в отрезках вида .

Для получения более полной информации обращайтесь к статье уравнение плоскости в отрезках , там показано приведение уравнения плоскости в отрезках к общему уравнению плоскости, там же Вы также найдете подробные решения характерных примеров и задач.

Нормальное уравнение плоскости.

Общее уравнение плоскости вида называют нормальным уравнением плоскости , если равна единице, то есть, , и .

Часто можно видеть, что нормальное уравнение плоскости записывают в виде . Здесь - направляющие косинусы нормального вектора данной плоскости единичной длины, то есть , а p – неотрицательное число, равное расстоянию от начала координат до плоскости.

Нормальное уравнение плоскости в прямоугольной системе координат Oxyz определяет плоскость, которая удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости . Если p=0 , то плоскость проходит через начало координат.

Приведем пример нормального уравнения плоскости.

Пусть плоскость задана в прямоугольной системе координат Oxyz общим уравнение плоскости вида . Это общее уравнение плоскости является нормальным уравнением плоскости. Действительно, и нормальный вектор этой плоскости имеет длину равную единице, так как .

Уравнение плоскости в нормальном виде позволяет находить расстояние от точки до плоскости .

Рекомендуем более детально разобраться с данным видом уравнения плоскости, посмотреть подробные решения характерных примеров и задач, а также научиться приводить общее уравнение плоскости к нормальному виду. Это Вы можете сделать, обратившись к статье .

Список литературы.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости . Если вы не знаете, что такое определитель, зайдите в первую часть урока - «Матрицы и определители ». Иначе вы рискуете ничего не понять в сегодняшнем материале.

Уравнение плоскости по трем точкам

Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:

Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:

M = (x 1 , y 1 , z 1);
N = (x 2 , y 2 , z 2);
K = (x 3 , y 3 , z 3);

Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:

Ax + By + Cz + D = 0

где числа A , B , C и D - коэффициенты, которые, собственно, и требуется найти.

Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ - подставить координаты в уравнение Ax + By + Cz + D = 0. Получится система из трех уравнений, которая легко решается.

Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.

Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.

Уравнение плоскости через определитель

Хватит лирики, приступаем к делу. Для начала - теорема о том, как связаны определитель матрицы и уравнение плоскости.

Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: M = (x 1 , y 1 , z 1); N = (x 2 , y 2 , z 2); K = (x 3 , y 3 , z 3). Тогда уравнение этой плоскости можно записать через определитель:

Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:

A 1 = (0, 0, 1);
B = (1, 0, 0);
C 1 = (1, 1, 1);

Составляем определитель и приравниваем его к нулю:

Раскрываем определитель:

a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x ) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;

Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные x , y и z шли в правильной последовательности. Вот и все! Уравнение плоскости готово!

Задача. Составьте уравнение плоскости, проходящей через точки:

A = (0, 0, 0);
B 1 = (1, 0, 1);
D 1 = (0, 1, 1);

Сразу подставляем координаты точек в определитель:

Снова раскрываем определитель:

a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y ) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;

Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется - чтобы упростить дальнейшее решение задачи.

Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель - и все, уравнение готово.

На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x 2 или x 3 , а в какой - просто x . Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.

Откуда берется формула с определителем?

Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.

Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:

M = (x 1 , y 1 , z 1);
N = (x 2 , y 2 , z 2);
K = (x 3 , y 3 , z 3).

Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:

T = (x , y , z )

Берем любую точку из первой тройки (например, точку M ) и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:

MN = (x 2 − x 1 , y 2 − y 1 , z 2 − z 1);
MK = (x 3 − x 1 , y 3 − y 1 , z 3 − z 1);
MT = (x − x 1 , y − y 1 , z − z 1).

Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы - и мы получим тот самый определитель, который указан в теореме:

Эта формула означает, что объем параллелепипеда, построенного на векторах MN , MK и MT , равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка T = (x , y , z ) - как раз то, что мы искали.

Замена точек и строк определителя

У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2 . Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:

Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T = (x ; y ; z ) в самом верху. Пожалуйста, если вам так удобно:

Некоторых смущает, что в одной из строчек присутствуют переменные x , y и z , которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:

Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:

Ax + By + Cz + D = 0

Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.

Задача. Составьте уравнение плоскости, проходящей через точки:

B 1 = (1, 0, 1);
C = (1, 1, 0);
D 1 = (0, 1, 1).

Итак, рассматриваем 4 точки:

B 1 = (1, 0, 1);
C = (1, 1, 0);
D 1 = (0, 1, 1);
T = (x , y , z ).

Для начала составим стандартный определитель и приравниваем его к нулю:

Раскрываем определитель:

a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z ) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;

Все, мы получили ответ: x + y + z − 2 = 0 .

Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x , y , z не внизу, а вверху:

Вновь раскрываем полученный определитель:

a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;

Мы получили точно такое же уравнение плоскости: x + y + z − 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.

Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.

В рассмотренной выше задаче мы использовали точку B 1 = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D 1 = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.

Всякое уравнение первой степени относительно координат x, y, z

Ax + By + Cz +D = 0 (3.1)

задает плоскость, и наоборот: всякая плоскость может быть представлена уравнением (3.1), которое называется уравнением плоскости .

Вектор n (A, B, C), ортогональный плоскости, называется нормальным вектором плоскости. В уравнении (3.1) коэффициенты A, B, C одновременно не равны 0.

Особые случаи уравнения (3.1):

1. D = 0, Ax+By+Cz = 0 - плоскость проходит через начало координат.

2. C = 0, Ax+By+D = 0 - плоскость параллельна оси Oz.

3. C = D = 0, Ax +By = 0 - плоскость проходит через ось Oz.

4. B = C = 0, Ax + D = 0 - плоскость параллельна плоскости Oyz.

Уравнения координатных плоскостей: x = 0, y = 0, z = 0.

Прямая в пространстве может быть задана:

1) как линия пересечения двух плоскостей,т.е. системой уравнений:

A 1 x + B 1 y + C 1 z + D 1 = 0, A 2 x + B 2 y + C 2 z + D 2 = 0; (3.2)

2) двумя своими точками M 1 (x 1 , y 1 , z 1) и M 2 (x 2 , y 2 , z 2), тогда прямая, через них проходящая, задается уравнениями:

= ; (3.3)

3) точкой M 1 (x 1 , y 1 , z 1), ей принадлежащей, и вектором a (m, n, р), ей коллинеарным. Тогда прямая определяется уравнениями:

. (3.4)

Уравнения (3.4) называются каноническими уравнениями прямой .

Вектор a называется направляющим вектором прямой .

Параметрические получим, приравняв каждое из отношений (3.4) параметру t:

x = x 1 + mt , y = y 1 + nt , z = z 1 + р t . (3.5)

Решая систему (3.2) как систему линейных уравнений относительно неизвестных x и y , приходим к уравнениям прямой в проекциях или к приведенным уравнениям прямой :

x = mz + a, y = nz + b. (3.6)

От уравнений (3.6) можно перейти к каноническим уравнениям, находя z из каждого уравнения и приравнивая полученные значения:

От общих уравнений (3.2) можно переходить к каноническим и другим способом, если найти какую-либо точку этой прямой и ее направляющий n = [n 1 , n 2 ], где n 1 (A 1 , B 1 , C 1) и n 2 (A 2 , B 2 , C 2) - нормальные векторы заданных плоскостей. Если один из знаменателей m, n или р в уравнениях (3.4) окажется равным нулю, то числитель соответствующей дроби надо положить равным нулю, т.е. система

равносильна системе ; такая прямая перпендикулярна к оси Ох.

Система равносильна системе x = x 1 , y = y 1 ; прямая параллельна оси Oz.

Пример 1.15 . Cоставьте уравнение плоскости, зная, что точка А(1,-1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.

Решение. По условию задачи вектор ОА (1,-1,3) является нормальным вектором плоскости, тогда ее уравнение можно записать в виде
x-y+3z+D=0. Подставив координаты точки А(1,-1,3), принадлежащей плоскости, найдем D: 1-(-1)+3 × 3+D = 0 Þ D = -11. Итак, x-y+3z-11=0.

Пример 1.16 . Составьте уравнение плоскости, проходящей через ось Оz и образующей с плоскостью 2x+y- z-7=0 угол 60 о.

Решение. Плоскость, проходящая через ось Oz, задается уравнением Ax+By=0, где А и В одновременно не обращаются в нуль. Пусть В не
равно 0, A/Bx+y=0. По формуле косинуса угла между двумя плоскостями

Решая квадратное уравнение 3m 2 + 8m - 3 = 0, находим его корни
m 1 = 1/3, m 2 = -3, откуда получаем две плоскости 1/3x+y = 0 и -3x+y = 0.

Пример 1.17. Составьте канонические уравнения прямой:
5x + y + z = 0, 2x + 3y - 2z + 5 = 0.

Решение. Канонические уравнения прямой имеют вид:

где m, n, р - координаты направляющего вектора прямой, x 1 , y 1 , z 1 - координаты какой-либо точки, принадлежащей прямой. Прямая задана как линия пересечения двух плоскостей. Чтобы найти точку, принадлежащую прямой, фиксируют одну из координат (проще всего положить, например, x=0) и полученную систему решают как систему линейных уравнений с двумя неизвестными. Итак, пусть x=0, тогда y + z = 0, 3y - 2z+ 5 = 0, откуда y=-1, z=1. Координаты точки М(x 1 , y 1 , z 1), принадлежащей данной прямой, мы нашли: M (0,-1,1). Направляющий вектор прямой легко найти, зная нормальные векторы исходных плоскостей n 1 (5,1,1) и n 2 (2,3,-2). Тогда

Канонические уравнения прямой имеют вид: x/(-5) = (y + 1)/12 =
= (z - 1)/13.

Пример 1.18 . В пучке, определяемом плоскостями 2х-у+5z-3=0 и х+у+2z+1=0, найти две перпендикулярные плоскости, одна из которых проходит через точку М(1,0,1).

Решение. Уравнение пучка, определяемого данными плоскостями, имеет вид u(2х-у+5z-3) + v(х+у+2z+1)=0, где u и v не обращаются в нуль одновременно. Перепишем уравнение пучка следующим образом:

(2u +v)x + (- u + v)y + (5u +2v)z - 3u + v = 0.

Для того, чтобы из пучка выделить плоскость, проходящую через точку М, подставим координаты точки М в уравнение пучка. Получим:

(2u+v) × 1 + (-u + v) × 0 + (5u + 2v) × 1 -3u + v =0, или v = - u.

Тогда уравнение плоскости, содержащей M, найдем, подставив v = - u в уравнение пучка:

u(2x-y +5z - 3) - u (x + y +2z +1) = 0.

Т.к. u ¹ 0 (иначе v=0, а это противоречит определению пучка), то имеем уравнение плоскости x-2y+3z-4=0. Вторая плоскость, принадлежащая пучку, должна быть ей перпендикулярна. Запишем условие ортогональности плоскостей:

(2u+ v) × 1 + (v - u) × (-2) + (5u +2v) × 3 = 0, или v = - 19/5u.

Значит, уравнение второй плоскости имеет вид:

u(2x -y+5z - 3) - 19/5 u(x + y +2z +1) = 0 или 9x +24y + 13z + 34 = 0.

В предыдущем разделе, посвященном плоскости в пространстве, мы рассмотрели вопрос с позиции геометрии. Теперь же перейдем к описанию плоскости с помощью уравнений. Взгляд на плоскость со стороны алгебры предполагает рассмотрение основных видов уравнения плоскости в прямоугольной системе координат O х у z трехмерного пространства.

Yandex.RTB R-A-339285-1

Определение уравнения плоскости

Определение 1

Плоскость – это геометрическая фигура, состоящая из отдельных точек. Каждой точке в трехмерном пространстве соответствуют координаты, которые задаются тремя числами. Уравнение плоскости устанавливает зависимость между координатами всех точек.

Уравнение плоскости в прямоугольной системе координат 0хуz имеет вид уравнения с тремя переменными х, у и z . Удовлетворяют уравнению координаты любой точки, лежащей в пределах заданной плоскости, не удовлетворяют координаты любых других точек, которые лежат вне заданной плоскости.

Подстановка в уравнение плоскости координат точки данной плоскости, обращает уравнение в тождество. При подстановке координат точки, лежащей вне плоскости, уравнение превращается в неверное равенство.

Уравнение плоскости может иметь несколько видов. В зависимости от специфики решаемых задач уравнение плоскости может быть записано по-разному.

Общее уравнение плоскости

Сформулируем теорему, а затем запишем уравнение плоскости.

Теорема 1

Всякая плоскость в прямоугольной системе координат O x y z в трехмерном пространстве может быть задана уравнением вида A x + B y + C z + D = 0 , где А, В, С и D – некоторые действительные числа, которые одновременно не равны нулю. Всякое уравнение, имеющее вид A x + B y + C z + D = 0 , определяет плоскость в трехмерном пространстве

Уравнение, имеющее вид A x + B y + C z + D = 0 носит название общего уравнения плоскости. Если не придавать числам А, В, С и D конкретных значений, то мы получаем уравнение плоскости в общем виде.

Важно понимать, что уравнение λ · A x + λ · B y + λ · C z + λ · D = 0 , будет точно так же определять плоскость. В уравнении λ - это некоторое отличное от нуля действительное число. Это значит, что равенства A x + B y + C z + D = 0 и λ · A x + λ · B y + λ · C z + λ · D = 0 равнозначны.

Пример 1

Общим уравнениям плоскости x - 2 · y + 3 · z - 7 = 0 и - 2 · x + 4 · y - 2 3 · z + 14 = 0 удовлетворяют координаты одних и тех же точек, расположенных в трехмерном пространстве. Это значит, что они задают одну и ту же плоскость.

Дадим пояснения к рассмотренной выше теореме. Плоскость и ее уравнение неразделимы, так как каждому уравнению A x + B y + C z + D = 0 соответствует плоскость в заданной прямоугольной системе координат, а каждой плоскости, расположенной в трехмерном пространстве, соответствует ее уравнение вида A x + B y + C z + D = 0 .

Уравнение плоскости A x + B y + C z + D = 0 может быть полным и неполным. Все коэффициенты А, B , С и D в полном уравнении отличны от нуля. В противном случае, общее уравнение плоскости считается неполным.

Плоскости, которые задаются неполными уравнениями, могут быть параллельны координатным осям, проходить через оси координат, совпадать с координатными плоскостями или располагаться параллельно им, проходить через начало координат.

Пример 2

Рассмотрим положение в пространстве плоскости, заданной уравнением 4 · y - 5 · z + 1 = 0 .

Она параллельна оси абсцисс и располагается перпендикулярно по отношению к плоскости O y z . Уравнение z = 0 определяет координатную плоскость O y z , а общее уравнение плоскости вида 3 · x - y + 2 · z = 0 соответствует плоскости, которая проходит через начало координат.

Важное уточнение: коэффициенты А, В и С в общем уравнении плоскости представляют собой координаты нормального вектора плоскости.

Когда говорят об уравнении плоскости, то подразумевают общее уравнение плоскости. Все виды уравнений плоскости, которые мы разберем в следующем разделе статьи, получают из общего уравнения плоскости.

Нормальное уравнение плоскости

Нормальное уравнение плоскости – это общее уравнение плоскости вида A x + B y + C z + D = 0 , которое удовлетворяет следующим условиям: длина вектора n → = (A , B , C) равна единице, т.е. n → = A 2 + B 2 + C 2 = 1 , а D ≤ 0 .

Также запись нормального уравнения плоскости может иметь следующий вид cos α · x + cos β · y + cos γ · z - p = 0 , где p – это неотрицательное число, которое равно расстоянию от начала координат до плоскости, а cos α , cos β , cos γ - это направляющие косинусы нормального вектора данной плоскости единичной длины.

n → = (cos α , cos β , cos γ) , n → = cos 2 α + cos 2 β + cos 2 γ = 1

То есть, согласно нормальному уравнению плоскости, плоскость в прямоугольной системе координат O х у z удалена от начала координат на расстояние p в положительном направлении нормального вектора этой плоскости n → = (cos α , cos β , cos γ) . Если p равно нулю, то плоскость проходит через начало координат.

Пример 3

Плоскость задана общим уравнением плоскости вида - 1 4 · x - 3 4 · y + 6 4 · z - 7 = 0 . D = - 7 ≤ 0 , нормальный вектор этой плоскости n → = - 1 4 , - 3 4 , 6 4 имеет длину, равную единице, так как n → = - 1 4 2 + - 3 4 2 + 6 4 = 1 . Соответственно, это общее уравнение плоскости является нормальным уравнением плоскости.

Для более детального изучения нормального уравнения плоскости мы рекомендуем перейти в соответствующий раздел. В теме приведены разборы задач и характерные примеры, а также способы приведения общего уравнения плоскости к нормальному виду.

Плоскость отсекает на координатных осях O х, O у и O z отрезки определенной длины. Длины отрезков задаются отличными от нуля действительными числами a , b и с. Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 . Знак чисел а, b и с показывает, в каком направлении от нулевого значения следует откладывать отрезки на координатных осях.

Пример 4

Построим в прямоугольной системе координат плоскость, которая задана уравнением формулы плоскости в отрезках x - 5 + y - 4 + z 4 = 1 .

Точки удалены от начала координат в отрицательном направлении на 5 единиц по оси абсцисс, на 4 единицы в отрицательном направлении по оси ординат и на 4 единицы в положительном направлении по оси аппликат. Отмечаем точки и соединяем их прямыми линиями.

Плоскость полученного треугольника является плоскостью, соответствующей уравнению плоскости в отрезках, имеющего вид x - 5 + y - 4 + z 4 = 1 .

Более подробно информация об уравнении плоскости в отрезках, приведении уравнения плоскости в отрезках к общему уравнению плоскости размещена в отдельной статье. Там же приведен ряд решений задач и примеров по теме.

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter